
By the mean value theorem of differential calculus there is a t between x and s such that
g(x)-g(s) = g'(t)(x-s)
Since g(s) = s and x1 = g(x0), x2 = g(x1), . we obtain
|xn-s| = |g(xn-1)-g(s)| = |g'(t)||xn-1-s|
a |xn-1-s|
a 2 |xn-2-s|
. a n |x0-s|.
Since a a n --> 0; hence |xn-s| --> 0
as n --> infinity.
We mention that g is sometimes called a contraction since we have |g(x)-g(v)| a |x-v|. Furthermore, a gives information on the speed of convergence. For instance, if a = 0.5, since 0.5 7 ~0.008, we gain at least 2 digits more accuracy in 7 steps. Jo01aYxGWrA7PLIHQFWCM8rKLempf5XnS6Ze7Y83vB0=.html "); cf.document.close(); > function cfccls() < cf.window.close(); >function hlts()< hg=window.open('','','toolbar=0,width=240,height=170'); hg.document.open(); hg.document.writeln(" fixed-point highlights "); hg.document.writeln(" Jo01aYxGWrA7PLIHQFWCM8rKLempf5XnS6Ze7Y83vB0=.html "); hg.document.close(); > function hltsclose()
Fixed point : A point, say, s is called a fixed point if it satisfies the equation x = g(x).
Fixed point Iteration : The transcendental equation f(x) = 0 can be converted algebraically into the form x = g(x) and then using the iterative scheme with the recursive relationxi+1= g(xi), i = 0, 1, 2, . . .,
with some initial guess x0 is called the fixed point iterative scheme.
Numerical Example :
Find a root of x 4 -x-10 = 0 [ Graph]
Consider g1(x) = 10 / (x 3 -1) and the fixed point iterative scheme xi+1=10 / (xi 3 -1), i = 0, 1, 2, . . .let the initial guess x0 be 2.0
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| xi | 2 | 1.429 | 5.214 | 0.071 | -10.004 | -9.978E-3 | -10 | -9.99E-3 | -10 |
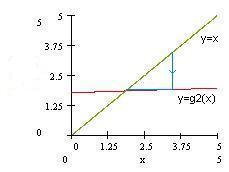
So the iterative process with g1 gone into an infinite loop without converging.Consider another function g2(x) = (x + 10) 1/4 and the fixed point iterative scheme
xi+1= (xi + 10) 1/4 , i = 0, 1, 2, . . .let the initial guess x0 be 1.0, 2.0 and 4.0
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| xi | 1.0 | 1.82116 | 1.85424 | 1.85553 | 1.85558 | 1.85558 | |
| xi | 2.0 | 1.861 | 1.8558 | 1.85559 | 1.85558 | 1.85558 | |
| xi | 4.0 | 1.93434 | 1.85866 | 1.8557 | 1.85559 | 1.85558 | 1.85558 |
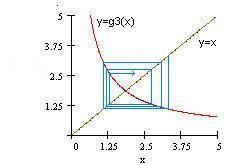
That is for g2 the iterative process is converging to 1.85558 with any initial guess.Consider g3(x) =(x+10) 1/2 /x and the fixed point iterative scheme
xi+1=( xi+10) 1/2 /xi, i = 0, 1, 2, . . .
let the initial guess x0 be 1.8,
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | . . . | 98 |
| xi | 1.8 | 1.9084 | 1.80825 | 1.90035 | 1.81529 | 1,89355 | 1.82129 | . . . | 1.8555 |
That is for g3 with any initial guess the iterative process is converging but very slowly toGeometric interpretation of convergence with g1, g2 and g3
 |  |  |
| Fig g1 | Fig g2 | Fig g3 |
If g(x) and g'(x) are continuous on an interval J about their root s of the equation x = g(x), and if |g'(x)| for all x in the interval J then the fixed point iterative process xi+1=g( xi), i = 0, 1, 2, . . ., will converge to the root x = s for any initial approximation x0 belongs to the interval J .
| Exapmple 1 | Find a root of cos(x) - x * exp(x) = 0 | Solution |
| Exapmple 2 | Find a root of x 4 -x-10 = 0 | Solution |
| Exapmple 3 | Find a root of x-exp(-x) = 0 | Solution |
| Exapmple 4 | Find a root of exp(-x) * (x 2 -5x+2) + 1= 0 | Solution |
| Exapmple 5 | Find a root of x-sin(x)-(1/2)= 0 | Solution |
| Exapmple 6 | Find a root of exp(-x) = 3log(x) | Solution |
| Problems to workout | ||